算法学习目录

时空复杂度分析

基础算法

排序
二分
高精度
前缀和与差分
双指针算法
位运算
离散化
区间合并

数据结构

链表与邻接表：树与图的存储
栈与队列：单调队列、单调栈
kmp
Trie
并查集
堆
Hash表

树状数组

线段树

搜索与图论

DFS与BFS
树与图的遍历：拓扑排序
最短路
最小生成树
二分图：染色法、匈牙利算法

数学知识

质数
约数
欧拉函数
快速幂
扩展欧几里得算法
中国剩余定理
高斯消元
组合计数
容斥原理
简单博弈论

动态规划

背包问题
线性DP
区间DP
计数类DP
数位统计DP
状态压缩DP
树形DP
记忆化搜索

贪心

时间复杂度和算法的选择

Pasted image 20211025132736

学习网站或资料

知乎算法专栏

基础算法

归并排序模板

//归并排序
int a[N],tmp[N];

void merge_sort(int a[],int l,int r)
{
    if(l>=r) return ;
    int mid = (l + r)/2;
    merge_sort(a,l,mid);
    merge_sort(a,mid+1,r);
    int k=0,i=l,j=mid+1;
    while(i<=mid && j<=r){
        if(a[i]<=a[j]){
            tmp[k++] = a[i++];
        }
        else 
            tmp[k++] = a[j++];
    }
    while(i<=mid) tmp[k++] = a[i++];
    while(j<=r) tmp[k++] = a[j++];
    for(int i=l,j=0; i<=r; ++i,++j){
        a[i] = tmp[j];
    }
}

快速排序模板

void quick_sort(int a[],int l,int r)
{
    if(l>=r) return ;
    int i = l-1, j = r+1, x = a[(l+r)/2];
    while(i<j){
        do i++; while(a[i]<x);
        do j--; while(a[j]>x);
        if(i < j) swap(a[i],a[j]);
    }
    
    quick_sort(a,l,j);
    quick_sort(a,j+1,r);
    return ;
}

数据结构

树状数组

树状数组原理

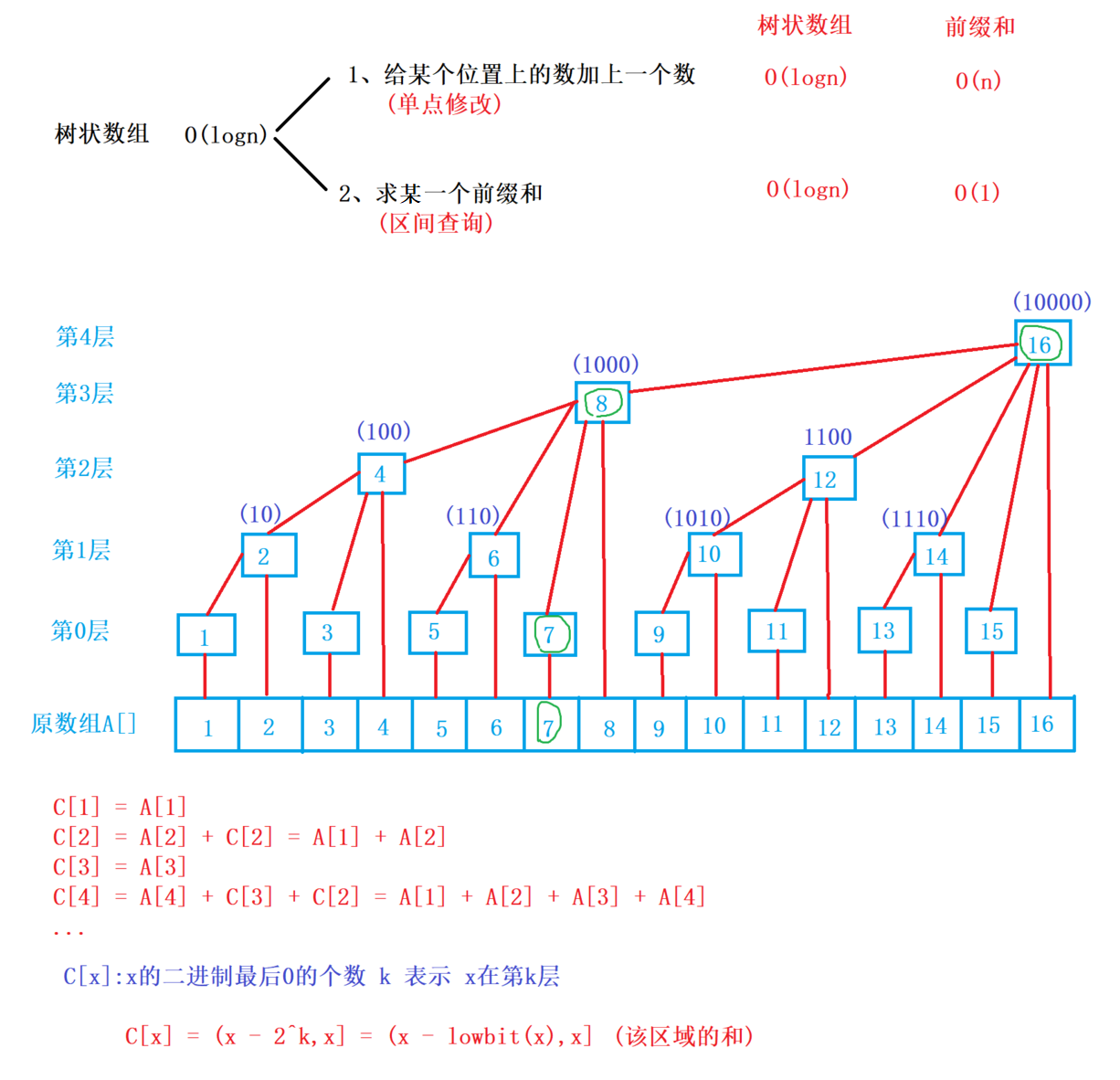
1、lowbit(x):返回x的最后一位1

2、add(x,v):在x位置加上v，并将后面相关联的位置也加上v

3、query(x):询问x的前缀和

时间复杂度 $O(logn)$

树状数组模板

const int N = 100005;
int a[N],tree[N];
int n,m;

int lowbit(int x)
{
    return x & (-x);
}
void update(int pos,int v)
{
    for(int i=pos; i0; pos-=lowbit(pos)) ans += tree[pos];
    return ans;
}
int query(int a,int b)
{
    return query(b) - query(a-1);
}

例题：1264. 动态求连续区间和

线段树

参见文章：线段树

树和图的存储

（数组建立邻接表）

邻接表

int h[N], e[N * 2], ne[N * 2], idx;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
//初始化
memset(h, -1, sizeof h);

图论

最短路知识结构

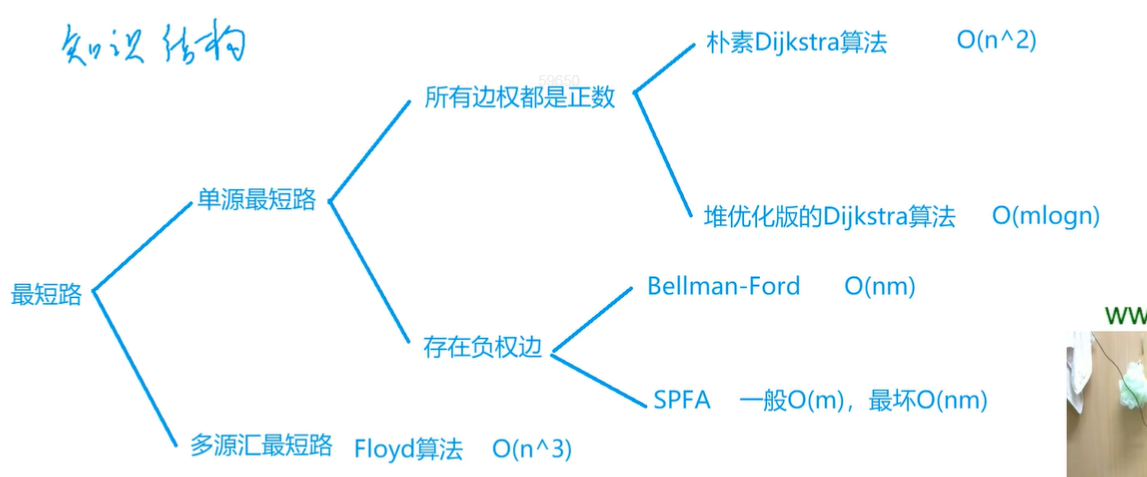
Dijkstra算法(迪杰斯特拉算法)

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;

int n,m;
int g[N][N];
int dist[N];
bool st[N];

int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    for(int i=0; i<n-1; ++i){
        int t = -1;
        for(int j=1; j<=n; ++j){
            if(!st[j] && (t==-1||dist[t]>dist[j]))
                t = j;
        }
        for(int j=1; j<=n; ++j){
            dist[j] = min(dist[j],dist[t]+g[t][j]);
        }
        st[t] = true;
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(g,0x3f,sizeof g);
    while (m -- ){
        int a,b,c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b],c);
    }
    printf("%d\n",dijkstra());
    return 0;
}

堆优化版的dijkstra()算法

#include <iostream>
#include <cstring>
#include <algorithm>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N = 1e6+10;
int h[N],e[N],w[N],ne[N],idx;
void add(int a,int b,int c)
{
    w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;  
}
int n,m;
int dist[N];
bool st[N];

int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    priority_queue<PII,vector<PII>,greater<PII> > heap;
    heap.push({0,1});
    while(heap.size())
    {
        auto t = heap.top(); heap.pop();
        int ver = t.second, distance = t.first;
        if(st[ver]) continue;
        st[ver] = true;
        
        for(int i=h[ver]; i!=-1; i=ne[i]){
            int j = e[i];
            
            if(dist[j] > dist[ver]+w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    else return dist[n];
}

int main()
{
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i=0; i<m; ++i){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a, b, c);
    }
    printf("%d\n",dijkstra());
    return 0;
}

bellman_ford()算法

证明：https://www.jianshu.com/p/b876fe9b2338

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 505, M = 10010;
struct Edge
{
    int a,b,c;
}edges[M];

int m,n,k,dist[N],last[N];

int bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
   
    for(int i=0; i<k; ++i){
        memcpy(last,dist,sizeof dist);
        for(int j=0; j<m; ++j){
            auto e = edges[j];
            dist[e.b] = min(dist[e.b],last[e.a]+e.c);
        }
    }
    if(dist[n]>0x3f3f3f3f/2) return 0x3f3f3f3f;
    else return dist[n];
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i=0; i<m; ++i){
        int a,b,c;
        scanf("%d%d%d", &a, &b,&c);
        edges[i]={a,b,c};
    }
    int ans = bellman_ford();
    if(ans==0x3f3f3f3f) puts("impossible");
    else printf("%d\n",ans);
    return 0;
}

spfa算法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;
const int N = 1e5+10;

int m,n;
int h[N],e[N],w[N],idx,ne[N];
int dist[N];
bool st[N];

void add(int a,int b,int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int spfa()
{
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size()){
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i=h[t]; i!=-1; i=ne[i]){
            int j = e[i];
            if(dist[j] > dist[t]+w[i]){
                dist[j] = dist[t] + w[i];
                if(!st[j]){
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return dist[n];
}
int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    while (m -- ){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a, b, c);
    }
    int t = spfa();
    if(t == 0x3f3f3f3f) puts("impossible");
    else printf("%d\n",t);
    
    return 0;
}

spfa算法判断是否有负环

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;
const int N = 2005,M=10005;
int n,m;
int h[N], e[M], ne[M], idx, w[M];
void add(int a,int b,int c)
{
    w[idx] = c, e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dist[N],cnt[N];
// bool st[N];

bool spfa()
{
    memset(dist,0x3f,sizeof(dist));
    dist[1] = 0;
    queue<int> q;
    for(int i=1; i<=n; ++i)
    {
        st[i] = true;
        q.push(i);
    }
    while(q.size())
    {
        int t = q.front();
        q.pop();
        // st[t] =false;
        for(int i=h[t]; i!=-1; i=ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t]+w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t]+1;
                if(cnt[j]>=n) return true;
                // if(!st[j]){
                    q.push(j);
                    // st[j] = true;
                // }
            }
        }
    }
    return false;
}

int main()
{
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    for(int i=0; i<m; ++i){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a, b, c);
    }
    if(spfa()) puts("Yes");
    else puts("No");
    return 0;
}

Floyd算法

void floyd()
{
    for(int k=1; k<=n; ++k){
        for(int i=1; i<=n; ++i){
            for(int j=1; j<=n; ++j){
                d[i][j] = min(d[i][j],d[i][k] + d[k][j]);
            }
        }
    }
}

数论

约数

约数个数定理和约数和定理

约数个数定理可以计算出一个数约数的个数，在小学奥数与中学竞赛中大有用处。
定理

对于一个大于1正整数n可以分解质因数

则n的正约数的个数就是

n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个==正约数的和==为
$f(n)=(p_1^0+p_1^1+p_1^2+…p_1^{a_1})(p_2^0+p_2^1+p_2^2+…p_2^{a_2})…(p_k^0+p_k^1+p_k^2+…p_k^{a_k}）$
其中a1、a2、a3…ak是p1、p2、p3，…pk的指数。

例题：
https://www.acwing.com/problem/content/872/
https://www.acwing.com/problem/content/873/

定理简证

首先同上，n可以分解质因数

,由约数定义可知的约数有:$p_1^0$, $p_1^1$, $p_1^2$, …,$p_1^{a_1}$ ，共（$a_1$+1）个；同理的约数有（$a_2$+1）个；……；的约数有（$a_k$+1）个。
故根据乘法原理：==n的约数的个数==就是(a1+1)(a2+1)(a3+1)…(ak+1)。
n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个==正约数的和==为

$f(n)=(p_1^0+p_1^1+p_1^2+…p_1^{a_1})(p_2^0+p_2^1+p_2^2+…p_2^{a_2})…(p_k^0+p_k^1+p_k^2+…p_k^{a_k}）$

欧拉函数

欧拉函数的定义

1∼N 中与 N 互质的数的个数被称为欧拉函数，记为 ϕ(N)。
若在算数基本定理中，$N=p^{a_1}_1p^{a_2}_2…p^{a_m}_m$，则：
$ϕ(N) = N×\frac{p1−1}{p1}×\frac{p2−1}{p2}×…×\frac{p_m−1}{p_m}$

例题：873. 欧拉函数

素数（质数）的筛法

1.最普通的筛法 O(nlogn)

C++ 代码

void get_primes2(){
    for(int i=2;i<=n;i++){

        if(!st[i]) primes[cnt++]=i;//把素数存起来
        for(int j=i;j<=n;j+=i){//不管是合数还是质数，都用来筛掉后面它的倍数
            st[j]=true;
        }
    }
}

2.诶氏筛法 O(nloglogn)

C++ 代码

void get_primes1(){
    for(int i=2;i<=n;i++){
        if(!st[i]){
            primes[cnt++]=i;
            for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉；
        }
    }
}

3.线性筛 O(n)

1)当 i % $primes[j]$ !=0 时,说明此时遍历到的 primes[j] 不是i的质因子，那么只可能是此时的primes[j]<i的最小质因子,所以$primes[j]*i$的最小质因子就是$primes[j]$;

2)当有 i%$primes[j]$==0 时,说明 i 的最小质因子是 $primes[j]$ ,因此$primes[j]*i$的最小质因子也就应该是 $prime[j]$，之后接着用 $st[primes[j+1]*i]=true$去筛合数时，就不是用最小质因子去更新了,因为i有最小质因子 $primes[j]<primes[j+1]$,此时的 $primes[j+1]$ 不是 $primes[j+1]*i$ 的最小质因子，此时就应该退出循环，避免之后重复进行筛选。

void get_primes(){
    //外层从2~n迭代，因为这毕竟算的是1~n中质数的个数，而不是某个数是不是质数的判定
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就没啥意义了
            st[primes[j]*i]=true;//用最小质因子去筛合数
            
//1)当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子，那么只可能是此时的primes[j]<i的
    //最小质因子,所以primes[j]*i的最小质因子就是primes[j];
//2)当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是
    //prime[j]，之后接着用st[primes[j+1]*i]=true去筛合数时，就不是用最小质因子去更新了,因为i有最小
    //质因子primes[j]<primes[j+1],此时的primes[j+1]不是primes[j+1]*i的最小质因子，此时就应该
     /退出循环，避免之后重复进行筛选。
            if(i%primes[j]==0) break;
        }
    }

}

作者：orzorz
链接：https://www.acwing.com/solution/content/7950/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

逆元

乘法逆元的定义

若整数 b，m 互质，并且对于任意的整数 a，如果满足 b|a，则存在一个整数 x，使得 $a/b≡a×x(mod\ m)$，则称 x 为 b 的模 m 乘法逆元，记为$b^{−1}(mod\ m)$。
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时，$b^{m−2}$ 即为 b 的乘法逆元

扩展欧几里得算法

裴蜀定理

裴蜀定理：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x、y，ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

或者这样解释：

裴蜀定理：对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：ax + by = m，有解当且仅当m是d的倍数。

并且ax+by=m的通解：

$\begin{cases}x_k = x k\cdot\displaystyle\frac{b}{\gcd(a,b)}\\y_k=y-k\cdot\displaystyle\frac{a}{\gcd(a,b)}\end{cases}(k\in \mathbb{Z})$

裴蜀定理及其证明

转载于 https://zhuanlan.zhihu.com/p/100567253 Pecco

下面hexo不支持图片内联，排版太乱，可直接跳过证明

（裴蜀定理）：设 $a, b$ 为正整数，则关于 $x,y$ 的方程 $ax by=c$ 有整数解当且仅当 c 是 $\gcd(a,b)$ 的倍数。

我们通过拓展欧几里得算法可以求得 ax+by=c 的一组解

并且ax+by=c的通解：

$\begin{cases}x_k = x k\cdot\displaystyle\frac{b}{\gcd(a,b)}\\y_k=y-k\cdot\displaystyle\frac{a}{\gcd(a,b)}\end{cases}(k\in \mathbb{Z})$

证明：

我们求得了的一组特解，那么通解是什么呢？

设除了已经求出的 $x,y$ 之外还有一组解 $x_1=x \delta$ 和 $y_1$ ，那么由 $ax_1-a\delta by=\gcd(a,b)$ ，得 $ax_1 b(y-\displaystyle\frac{a\delta}{b})=\gcd(a,b)$ ，得 $y_1=y-\displaystyle\frac{a\delta}{b}$ 。

但是，我们必须要保证 $\delta$ 和 $\displaystyle\frac{a\delta}{b}$ 都是整数，后者等于 $\displaystyle\frac{a'}{b'}\delta$ ，其中 $a'=\displaystyle\frac{a}{\gcd(a,b)}$ ， $b'=\displaystyle\frac{b}{\gcd(a,b)}$ 。由于 $a'$ 与 $b'$ 互质， $\delta$ 应当等于 $kb'$ （ $k$ 是整数），即：

$\begin{cases}x_k = x k\cdot\displaystyle\frac{b}{\gcd(a,b)}\\y_k=y-k\cdot\displaystyle\frac{a}{\gcd(a,b)}\end{cases}(k\in \mathbb{Z})$

这便是该不定方程的通解

转载于 https://zhuanlan.zhihu.com/p/100567253 Pecco

拓展欧几里得算法

拓展欧几里得算法：它可以在辗转相除途中求出不定方程 $ax by=c$ 的一组解。

公式推导如下：

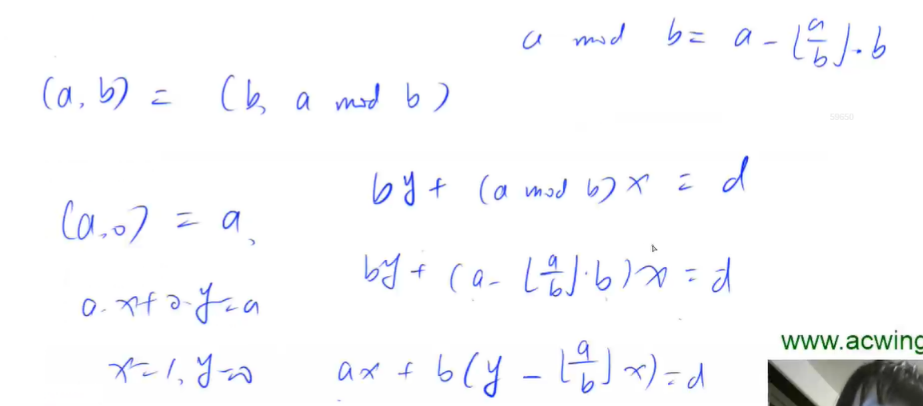
代码模板：

/*
ax+by=d
bx+(a%b)y=d
bx+(a-a/b*b)y=d
ay+b(x-a/b*y)=d
{
    x=y
    y=x-a/b*y
}
*/
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0){
        x = 1,y = 0;
        return a;
    }
    int d = exgcd(b,a%b,x,y);
    int x0 = x,y0 = y;
    x = y0;
    y = x0 - a/b * y0;
    return d;
}

葛济维

http://gjwhhhh.github.io/2021/11/26/suan-fa-bi-ji/

本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源葛济维 !

笔记算法模板

JavaGuide阅读笔记

2021-11-28 笔记

Java 面试

付账问题（贪心问题、均值不等式）

2021-11-23 算法

蓝桥杯贪心均值不等式

算法笔记（长期更新）

算法学习目录

时间复杂度和算法的选择

学习网站或资料

基础算法

归并排序模板

快速排序模板

数据结构

树状数组

树状数组原理

树状数组模板

线段树

树和图的存储

邻接表

图论

最短路知识结构

Dijkstra算法(迪杰斯特拉算法)

堆优化版的dijkstra()算法

bellman_ford()算法

spfa算法

spfa算法判断是否有负环

Floyd算法

数论

约数

约数个数定理和约数和定理

欧拉函数

素数（质数）的筛法

1.最普通的筛法 O(nlogn)

2.诶氏筛法 O(nloglogn)

3.线性筛 O(n)

逆元

乘法逆元的定义

扩展欧几里得算法

裴蜀定理

裴蜀定理及其证明

拓展欧几里得算法

你的赏识是我前进的动力