糖果传递（贪心）——《算法竞赛进阶指南》,微软面试题 , HAOI2008

糖果传递（贪心）

糖果传递

有 n 个小朋友坐成一圈，每人有 a[i] 个糖果。

每人只能给左右两人传递糖果。

每人每次传递一个糖果代价为 1。

求使所有人获得均等糖果的最小代价。

输入格式
第一行输入一个正整数 n，表示小朋友的个数。

接下来 n 行，每行一个整数 a[i]，表示第 i 个小朋友初始得到的糖果的颗数。

输出格式
输出一个整数，表示最小代价。

数据范围
1≤n≤1000000,
0≤a[i]≤2×109,
数据保证一定有解。

输入样例：
4
1
2
5
4
输出样例：
4

题解

首先，最终每个小朋友的糖果数量可以计算出来，等于糖果总数除以n，用 $\overline{a}$ 表示。
假设标号为i的小朋友开始有ai颗糖果，Xi表示第i个小朋友给了第i-1个小朋友Xi颗糖果，如果Xi<0，说明第i-1个小朋友给了第i个小朋友Xi颗糖果，X1表示第一个小朋友给第n个小朋友的糖果数量。 所以最后的答案就是ans=|X1| + |X2| + |X3| + ……+ |Xn|。

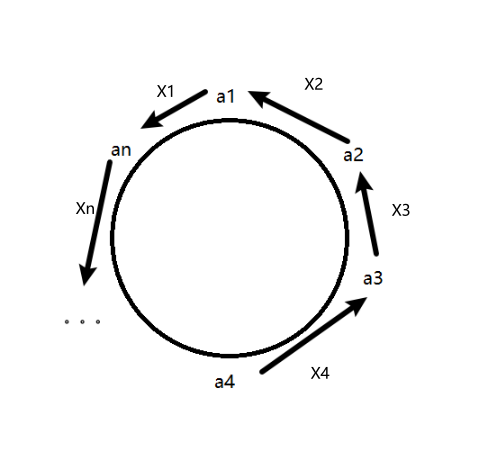
对于第一个小朋友，他给了第n个小朋友X1颗糖果，还剩a1-X1颗糖果；但因为第2个小朋友给了他X2颗糖果，所以最后还剩a1-X1+X2颗糖果。根据题意，最后的糖果数量等于$\overline{a}$，即得到了一个方程：a1-X1+X2= $\overline{a}$ 。

其他的方程如下列方程所示：并带入求解

$
\begin{cases}
a_1-X_1+X_2=\overline{a}\
a_2-X_2+X_3=\overline{a}\
a_3-X_3+X_4=\overline{a}\
……\
a_n-X_n+X_1=\overline{a}\
\end{cases}
$ => $\begin{cases}
X_1=X_1\
X_2=\overline{a}-a_1+X_1\
X_3=\overline{a}-a_2+X_2=\overline{a}-a_2+\overline{a}-a_1+X_1\
X_4=X_1-((a_1+a_2+a_3)-3*\overline{a})\
……\
X_n=X_1-((a_1+a_2+…+a_{n-1})-(n-1)*\overline{a})\
\end{cases}$

设$C_n=(a_1+a_2+…+a_{n-1})-(n-1)*\overline{a}$

易得：$C_n=C_{n-1}+a_{n-1}-\overline{a}$ ，$C_1=0$

因此最后的答案为 ans=|X1-C1| + |X1-C2| + |X1-C3| + ……+ |X1-Cn|。

此表达式的意思为求一个点 X1 到n个点距离之和最小，求解中位数就是X1,然后计算代价就行。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e6+5;
typedef long long LL;

int a[N],c[N];

int main()
{
    int n;
    scanf("%d", &n);
    LL sum = 0;  //平均数
    for (int i = 1; i <= n; i ++ ){
        scanf("%d", &a[i]);
        sum += a[i];
    }
    sum /= n;
    c[1] = 0;
    for(int i=2; i<=n; ++i){
        c[i] = c[i-1]+a[i-1]-sum;
    }
    sort(c+1,c+n+1);
    LL ans = 0; 
    
    for(int i=1; i<=n; ++i){
        ans += abs(c[i]-c[(n+1)/2]);    
    }
    printf("%lld\n",ans);
    return 0;
}