树状数组原理
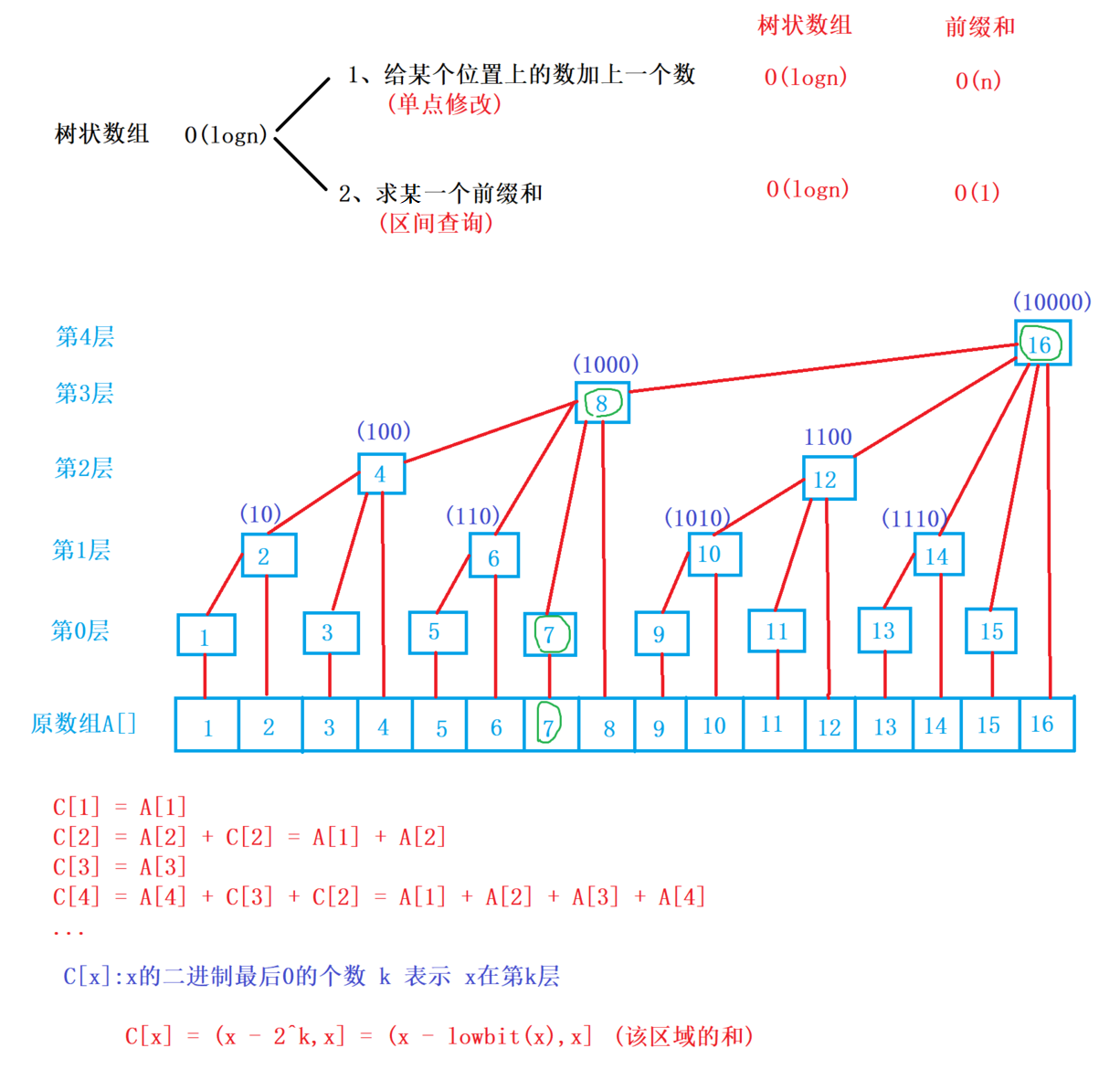
1、lowbit(x):返回x的最后一位1
2、add(x,v):在x位置加上v,并将后面相关联的位置也加上v
3、query(x):询问x的前缀和
时间复杂度 $O(logn)$
树状数组模板
const int N = 100005;
int a[N],tree[N];
int n,m;
int lowbit(int x)
{
return x & (-x);
}
void update(int pos,int v)
{
for(int i=pos; i0; pos-=lowbit(pos)) ans += tree[pos];
return ans;
}
int query(int a,int b)
{
return query(b) - query(a-1);
}



